因果推論を実践するための基礎的なツールについて理解を深めたい。初学者は次の5つのツールを知っておくと良いだろう。
- DAG
- 回帰分析
- 層化解析法
- マッチング
- 傾向スコア
DAG
DAG(非巡回的有向グラフ、Directed Acyclic Graph)は、Pearl学派の統計的因果推論における基本にして大本命となるツールである。そもそも因果関係を厳密に取り扱うためにはSCM(構造的因果モデル、Structual Causal Model)による関数表現が必要になる。例えば、体育の授業におけるバスケットボールの成績は身長と性別から次のように表現可能である。
- V={身長, 性別, バスケの成績}, U={U1, U2, U3}, F={f1, f2}
- 性別 = U1
- 身長 = f1(性別, U2)
- バスケの成績 = f2(身長, 性別, U3)
しかし、これでは「バスケの成績」と「身長」・「体重」の因果関係を直感的に理解することはなかなか難しい。また、因果関係にある現象は必ずしもすべてこのような形で定量的に理解し関数表記できるわけではなく、むしろその現象に対して定性的な理解しか持てないことのほうが多い。
そのような場合にも、グラフィカルモデル(グラフ)によってそれぞれの変数間の関係を表すことができる。
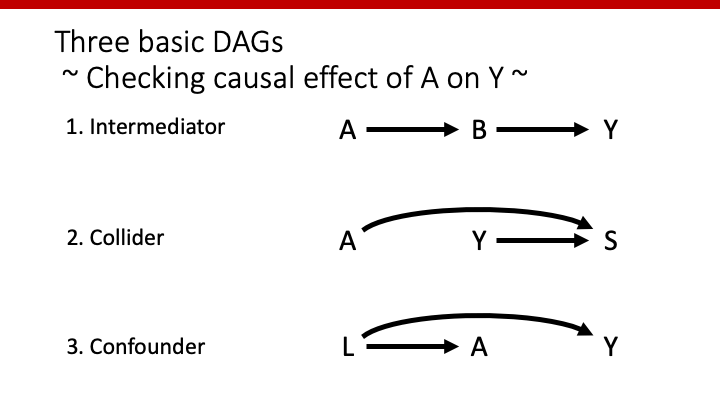
DAGとは上図のように、因果関係をグラフで定義したものである。例えば、X(風邪薬を飲むこと)とY(風邪が治ること)を X → Y のように表し、原因Xと結果Yを矢印で結ぶ。XがYの子であれば、YはXの直接原因となる。
Pearl曰く、(線形システムを仮定した)グラフ理論にもとづくと、DAGだけでかなり多くのことを議論できる。ただし、グラフを使った議論は古典的な統計学に比べ新しい概念で馴染まれにくい。Rubinによる代数的な因果推論の取り扱いのほうが(もしかすると)とっつきやすいのかもしれない。
いずれにしても、現象を整理し正しく理解するためにはDAGは必須のツールである。適切なDAGを描くことができなければ、その現象を定性的に説明することも、定量的に評価することもできない。
回帰分析
データ分析をしているとごくごく自然と回帰分析をしてみたくなるものだ。回帰分析はその手軽さと分かりやすさから広く一般に普及しているが、統計的因果推論的観点から回帰分析を考えるとどうなるだろう。
まずは回帰分析の定義から。
回帰分析:結果変数 Y をm個の説明変数 X1, …, Xm で説明する線形回帰モデル
- Y = β0 + β1X1 + … + βmXm + ε
- ε は誤差項で、N(0, σ^2) に従うと仮定されることが多い。
- E[Y] = β0 + β1X1 + … + βmXm
ここで、いくつかのDAGについて、それらを回帰分析的に定式化(モデル化)するとどのようになるか、みてみよう。
- U ↘
X → Y - Y = α + βX + γU + ε
- ※ Uが観測されない場合:Y = α + βX + ε
- ↙ U
X → Y - Y = α + βX + ε
- Xの値で条件が付されており、Uの影響はYに及ばない
- ↙ U ↘
X → Y - Uは交絡因子
- Xの回帰係数がXの単独の効果を必ずしも表さないため注意が必要
- 交絡因子の分だけ偏りが生じるため、できる限り多くの交絡因子を特定する
最後に、回帰分析を使った適切なモデル選択の例を紹介する。この例は岩崎 学『統計的因果推論』からの抜粋である。
ある大学のある学科では、「応用統計学」の授業を3年次に開講していて、2人の教員AとBがそれぞれ1クラスずつを受け持っている(以降これらをクラスA、クラスBと呼ぶ)。学生は自らの意思でクラスAかクラスBを選択して履修する。今年度、両クラスとも30名ずつの学生が履修し、同じ問題で学期の最後に期末試験を実施したところ、クラスAでの平均は約68点、クラスBでの平均は約79点と、両クラス間で約11点の開きがあった。
果たしてクラスAとクラスBで生じた期末試験の点数の差は、クラスの違い(クラス間の教え方の違い)に依るものだろうか。
ここで、次のような変数を準備し、いくつかのモデルを作成してみることにした。
- Z: クラスを表すダミー変数(0: クラスA、1: クラスB)
- X1: 前年度の学生の成績(GPA)
- X2: 今年度実施の中間試験の点数(両クラスとも同じ問題)
- Y: 期末試験の点数(両クラスとも同じ問題)
- Y = α + τZ + β1X1 + β2X2 + ε
モデル化の結果は上表の通りであったとする。ただし各セルの値は各モデルでの切片と各回帰係数の値、()内はP値、R列は決定係数の値を示す。
このモデル化の目的が期末試験の点数を予測するモデルを作成することであれば、Rの値からZとX2を使用したモデル、またはZとX1とX2を使用したモデルが適切であろう。しかしここでは、クラスAとクラスBの教え方の違いが期末試験の点数にどう影響したのかを見極めたい。
ZとX1を使用したモデルを見てほしい。Zの値が約2点程度になっていることから、クラスの違いによる点数の差異は、単純な平均値比較の場合の約11点程度はとても過大に評価されていたことがわかる。それにP値の値が高いことから、Zのモデルへの寄与度(信頼性)も怪しい。
よってこの例では、クラス間の教え方によって期末試験の点数に差が生まれたわけではなく、なんらかの理由でもともと成績の良い人(賢い人)がクラスBを、そうでない人がクラスAを選択しただけである、と言えそうである。



0 コメント